ELASTICIDAD
En física el término elasticidad designa la propiedad mecánica de ciertos materiales de sufrir deformaciones reversibles cuando se encuentran sujetos a la acción de fuerzas exteriores y de recuperar la forma original si estas fuerzas exteriores se eliminan.

Una varilla elástica vibrando, es un ejemplo de sistema donde la energía potencial elástica se transforma en energía cinética y viceversa.
La elasticidad es estudiada por la teoría de la elasticidad, que a su vez es parte de la mecánica de sólidos deformables. La teoría de la elasticidad (TE) como la mecánica de sólidos (MS) deformables describe cómo un sólido (o fluido totalmente confinado) se mueve y deforma como respuesta a fuerzas exteriores. La diferencia entre la TE y la MS es que la primera solo trata sólidos en que las deformaciones son termodinámicamente reversibles y en los que el estado tensiones  en un punto
en un punto  en un instante dado dependen solo de las deformaciones
en un instante dado dependen solo de las deformaciones 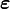 en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcionalmente es de la forma:
en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcionalmente es de la forma:
 en un punto
en un punto  en un instante dado dependen solo de las deformaciones
en un instante dado dependen solo de las deformaciones 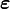 en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcionalmente es de la forma:
en el mismo punto y no de las deformaciones anteriores (ni el valor de otras magnitudes en un instante anterior). Para un sólido elástico la ecuación constitutiva funcionalmente es de la forma:
donde  denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.
denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.
 denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.
denota el conjunto de tensores simétricos de segundo orden del espacio euclídeo. Si el sólido es homogéneo el valor de la función anterior no dependerá del segundo argumento.La propiedad elástica de los materiales está relacionada, como se ha mencionado, con la capacidad de un sólido de sufrir transformaciones termodinámicas reversibles e independencia de la velocidad de deformación (los sólidos viscoelásticos y los fluidos, por ejemplo, presentan tensiones dependientes de la velocidad de deformación). Cuando sobre un sólido deformable actúan fuerzas exteriores y éste se deforma se produce un trabajo de estas fuerzas que se almacena en el cuerpo en forma de energía potencial elástica y por tanto se producirá un aumento de la energía interna.
El sólido se comportará elásticamente si este incremento de energía puede realizarse de forma reversible, en este caso se dice que el sólido es elástico.

Componentes del tensor tensión en un punto P de un sólido deformable.

Componentes del tensor tensión en un punto P de un sólido deformable.
Elasticidad lineal
Un caso particular de sólido elástico se presenta cuando las tensiones y las deformaciones están relacionadas linealmente, mediante la siguiente ecuación constitutiva:
Cuando eso sucede se dice que el sólido es elástico lineal. La teoría de la elasticidad lineal es el estudio de sólidos elásticos lineales sometidos a pequeñas deformaciones de tal manera que además los desplazamientos y deformaciones sean "lineales", es decir, que las componentes del campo de desplazamientos u sean muy aproximadamente una combinación lineal de las componentes del tensor deformación del sólido. En general un sólido elástico lineal sometido a grandes desplazamientos no cumplirá esta condición. Por tanto la teoría de la elasticidad lineal solo es aplicable a:
- Sólidos elásticos lineales, en los que tensiones y deformaciones estén relacionadas linealmente (linealidad material).
- Deformaciones pequeñas, es el caso en que deformaciones y desplazamientos están relacionados linealmente. En este caso puede usarse el tensor deformación lineal de Green-Lagrange para representar el estado de deformación de un sólido (linealidad geométrica).
Debido a los pequeños desplazamientos y deformaciones a los que son sometidos los cuerpos, se usan las siguientes simplificaciones y aproximaciones para sistemas estables:
- Las tensiones se relacionan con las superficies no deformadas
- Las condiciones de equilibrio se presentan para el sistema no deformado
Para determinar la estabilidad de un sistema hay presentar las condiciones de equilibrio para el sistema deformado.
Tensión
La tensión en un punto se define como el límite de la fuerza aplicada sobre una pequeña región sobre un plano π que contenga al punto dividida del área de la región, es decir, la tensión es la fuerza aplicada por unidad de superficie y depende del punto elegido, del estado tensional de sólido y de la orientación del plano escogido para calcular el límite. Puede probarse que la normal al plano escogido nπ y la tensión tπ en un punto están relacionadas por:

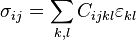

No hay comentarios:
Publicar un comentario