DENSIDAD
En física y química, la densidad (del latín densĭtas, -ātis) es una magnitud escalar referida a la cantidad de masa en un determinado volumen de una sustancia. Usualmente se simboliza mediante la letra rho ρ del alfabeto griego. La densidad media es la razón entre la masa de un cuerpo y el volumen que ocupa.
Si un cuerpo no tiene una distribución uniforme de la masa en todos sus puntos la densidad alrededor de un punto puede diferir de la densidad media. Si se considera una sucesión pequeños volúmenes decrecientes 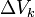 (convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo
(convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo  la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
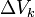 (convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo
(convergiendo hacia un volumen muy pequeño) y estén centrados alrededor de un punto, siendo  la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
la masa contenida en cada uno de los volúmenes anteriores, la densidad en el punto común a todos esos volúmenes:
Como ejemplo, un objeto de plomo es más denso que otro de corcho, con independencia del tamaño y masa.
Tipos de densidad;
Densidad absoluta:
 , la densidad; m, la masa; y V, el volumen de la sustancia.
, la densidad; m, la masa; y V, el volumen de la sustancia.Densidad relativa:
La densidad relativa de una sustancia es la relación existente entre su densidad y la de otra sustancia de referencia; en consecuencia, es una magnitud adimensional (sin unidades)
donde 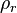 es la densidad relativa,
es la densidad relativa,  es la densidad de la sustancia, y
es la densidad de la sustancia, y  es la densidad de referencia o absoluta.
es la densidad de referencia o absoluta.
Para los líquidos y los sólidos, la densidad de referencia habitual es la del agua líquida a la presión de 1 atm y la temperatura de 4 °C. En esas condiciones, la densidad absoluta del agua destilada es de 1000 kg/m³, es decir, 1 kg/dm³.
Para los gases, la densidad de referencia habitual es la del aire a la presión de 1 atm y la temperatura de 0 °C.
Cambios de densidad:
En general, la densidad de una sustancia varía cuando cambia la presión o la temperatura, y en los cambios de estado. En particular se ha establecido empíricamente:
 es la constante universal de los gases ideales,
es la constante universal de los gases ideales,  es la presión del gas,
es la presión del gas,  su masa molar y
su masa molar y 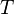 la temperatura absoluta. Eso significa que un gas ideal a 300 K (27 °C) y 1 atm duplicará su densidad si se aumenta la presión a 2 atm manteniendo la temperatura constante o, alternativamente, se reduce su temperatura a 150 K manteniendo la presión constante. Como puede comprobarse las relaciones () también se satisfacen en ()
la temperatura absoluta. Eso significa que un gas ideal a 300 K (27 °C) y 1 atm duplicará su densidad si se aumenta la presión a 2 atm manteniendo la temperatura constante o, alternativamente, se reduce su temperatura a 150 K manteniendo la presión constante. Como puede comprobarse las relaciones () también se satisfacen en ()
- Cuando aumenta la presión, la densidad de cualquier material estable también aumenta.
- Como regla general, al aumentar la temperatura, la densidad disminuye (si la presión permanece constante). Sin embargo, existen notables excepciones a esta regla. Por ejemplo, la densidad del agua dulce crece entre el punto de fusión (a 0 °C) y los 4 °C; algo similar ocurre con el silicio a bajas temperaturas.[cita requerida]
(*)Por otro lado, la densidad de los gases es fuertemente afectada por la presión y la temperatura. La ley de los gases ideales describe matemáticamente la relación entre estas tres magnitudes:
(**)donde
 es la constante universal de los gases ideales,
es la constante universal de los gases ideales,  es la presión del gas,
es la presión del gas,  su masa molar y
su masa molar y 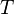 la temperatura absoluta. Eso significa que un gas ideal a 300 K (27 °C) y 1 atm duplicará su densidad si se aumenta la presión a 2 atm manteniendo la temperatura constante o, alternativamente, se reduce su temperatura a 150 K manteniendo la presión constante. Como puede comprobarse las relaciones () también se satisfacen en ()
la temperatura absoluta. Eso significa que un gas ideal a 300 K (27 °C) y 1 atm duplicará su densidad si se aumenta la presión a 2 atm manteniendo la temperatura constante o, alternativamente, se reduce su temperatura a 150 K manteniendo la presión constante. Como puede comprobarse las relaciones () también se satisfacen en ()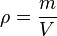
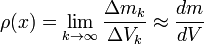
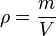
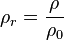

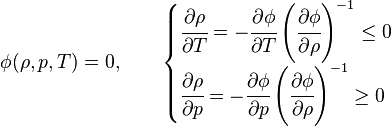
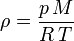
No hay comentarios:
Publicar un comentario