EMPUJE
El empuje es una fuerza de reacción descrita cuantitativamente por la tercera ley de Newton. Cuando un sistema expele o acelera masa en una dirección (acción), la masa acelerada causará una fuerza igual en dirección contraria (reacción). Matemáticamente esto significa que la fuerza total experimentada por un sistema se acelera con una masa m que es igual y opuesto a m veces la aceleración a, experimentada por la masa:
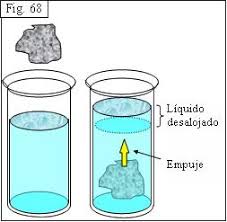
La fuerza de empuje es una fuerza que aparece cuando se sumerge un cuerpo en un fluido. El módulo de ésta viene dado por el peso del volumen del fluido desalojado.
Se produce debido a que la presión de cualquier fluido en un punto determinado depende principalmente de la profundidad en que éste se encuentre (en otras palabras, a la cantidad de fluido que tenga encima).
Esta presión ejerce una fuerza sobre cualquier cuerpo sumergido en el fluido y tiene la propiedad ser perpendicular a la superficie del cuerpo.
Si pensamos en un cuerpo cúbico sumergido es evidente que alguna de sus caras estará más profunda que el resto de ellas. Dado que la presión ejerce una fuerza sobre todas las caras sin importar cual sea y siempre perpendicular a esta, la fuerza que se ejerce sobre la cara más profunda es mayor que la fuerza sobre la cara menos profunda, lo que da como resultante una fuerza ascendente que es la fuerza de empuje.
En las caras laterales no ocurre esto ya que las fuerzas laterales se restan puesto que, punto a punto, se encuentran a la misma altura.

Se produce debido a que la presión de cualquier fluido en un punto determinado depende principalmente de la profundidad en que éste se encuentre (en otras palabras, a la cantidad de fluido que tenga encima).
Esta presión ejerce una fuerza sobre cualquier cuerpo sumergido en el fluido y tiene la propiedad ser perpendicular a la superficie del cuerpo.
Si pensamos en un cuerpo cúbico sumergido es evidente que alguna de sus caras estará más profunda que el resto de ellas. Dado que la presión ejerce una fuerza sobre todas las caras sin importar cual sea y siempre perpendicular a esta, la fuerza que se ejerce sobre la cara más profunda es mayor que la fuerza sobre la cara menos profunda, lo que da como resultante una fuerza ascendente que es la fuerza de empuje.
En las caras laterales no ocurre esto ya que las fuerzas laterales se restan puesto que, punto a punto, se encuentran a la misma altura.

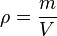
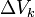

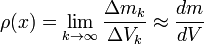
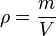
 , la densidad; m, la masa; y V, el volumen de la sustancia.
, la densidad; m, la masa; y V, el volumen de la sustancia.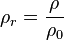
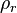


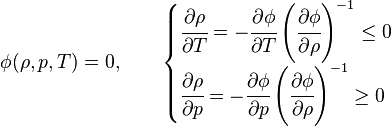
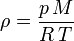
 es la
es la  es la presión del gas,
es la presión del gas,  su
su 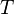 la
la  sobre el émbolo de menor área
sobre el émbolo de menor área 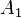 se genera una presión
se genera una presión  :
:
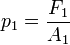
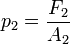
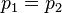
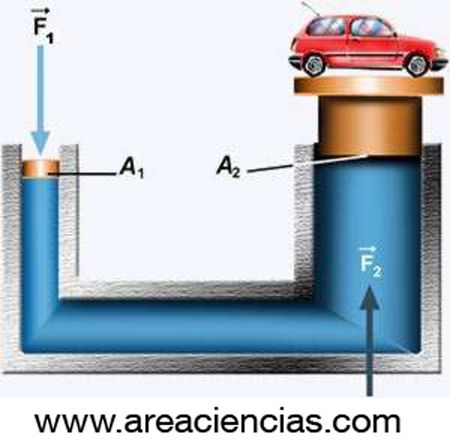
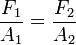 y la relación de fuerzas:
y la relación de fuerzas: 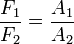

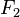 = fuerza del émbolo mayor en N.
= fuerza del émbolo mayor en N.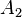 = área del émbolo mayor en m².
= área del émbolo mayor en m².